

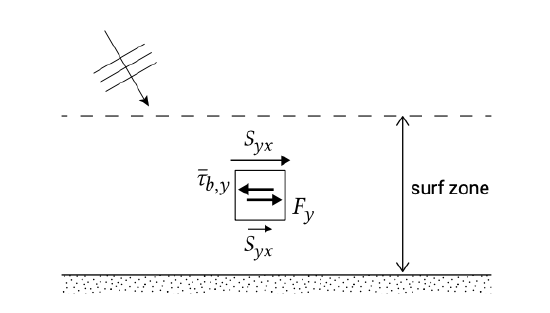
In the alongshore direction the transfer of momentum from the wave motion to the mean flow gives rise to a longshore current. Note that besides this wave-induced (due to wave dissipation in the breaker zone) current, also tidal and wind forces can generate a current along the coast. These are discussed in Sect. 5.6 and Sect. 5.7.2. The longshore current (velocity magnitude and cross-shore distribution) is an import- ant input parameter in longshore sediment transport computations. Alongshore momentum balance (straight, parallel depth contours) We consider again the 2D situation (see Fig. 5.4) of a long-crested wave obliquely incident to an alongshore uniform coast (\(\theta = \varphi\) and all \(y\)-derivatives are zero). The cross-shore rate of variation of the shear component of the radiation stress \(S_\) acts as a driving force (Eq. 5.5.3.4). In the cross-shore direction the balancing force was supplied by a hydraulic pressure gradient. However, for an infinitely long uninterrupted coast- line, no such hydraulic pressure gradient can develop in the alongshore direction. The counterforce restoring equilibrium therefore must be supplied by bed shear stresses that develop when a longshore current is generated. The bottom shear stress restrains the current and is non-zero only in the presence of a current. Note that in the cross-shore direction the bed shear stress associated with the mean current was assumed small as compared to the pressure force. We only consider the stationary situation. The alongshore component of the momentum balance for a steady state and alongshore uniformity can be written as: \[F_y = -\dfrac
Analytical model for alongshore wave force in the surf zone
To find an easy analytical expression for the longshore current we assume again the simple model for wave dissipation due to breaking that relates the wave height to the local water depth: \(H =\gamma h\) for every water depth in the surf zone. An alternative would be solving the energy balance numerically. The analytical expression is calculated from the dissipation model and Snell’s law:
\[F_y = -\dfrac \dfrac Ec_g \cos \varphi = -\dfrac \dfrac 1/8 \rho g \gamma^2 h^2 c_g \cos \varphi\]
In shallow water \(c_g = c = \sqrt\) and since due to refraction \(\varphi\) is small (generally around 10° to 15°) we assume \(\cos \varphi \approx 1\). We now have:
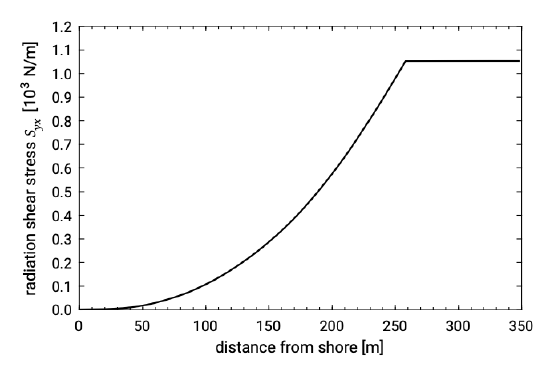
As mentioned above the radiation shear stress \(S_\) is constant seaward of the border of the breaker zone (thus the wave force is zero). It decreases inside the breaker zone to zero at the waterline (see Fig. 5.37).
For many day to day wave conditions, this gradient in \(S_\) causes alongshore stresses (forces) which are in the same order of magnitude as the bottom shear stress in rivers: in the order of \(1\ N/m^2\) to \(10\ N/m^2\). The cross-shore gradient in the alongshore radiation stress \(S_\) is therefore an important driving force in the littoral zone.
Quadratic friction law for bed shear stress
The next step is the formulation of the bed shear stress. In Sect. 5.4.3 we have already discussed the quadratic friction law for wave and current only situations. For currents the turbulence is present in the entire water column. The turbulence due to waves is present in the wave boundary layer only and significantly increases the bed shear stress. This is not only due to the significant increase in friction factors but due to the velocity being generally higher in the wave motion. For the vertical profile of the longshore current we need a quadratic resistance law of combined current and wave action. Such a law is non-trivial since:
For the reasons mentioned above many different models exist for the bed shear stress under waves and currents. Depending on the model, the relative contributions of waves and currents to the bed shear stress vary. Some models describe the time-averaged bed shear stress, others the instantaneous bed shear stress. The description of the sediment transport requires an accurate (intra-wave or time-averaged, depending on the sediment transport model) bed shear stress. Therefore in Sect. 6.5 the bed shear stress is treated in more detail.
For the determination of the time-averaged bed shear stress in the alongshore direction, necessary to compute the longshore current, we take a fairly simple approach:
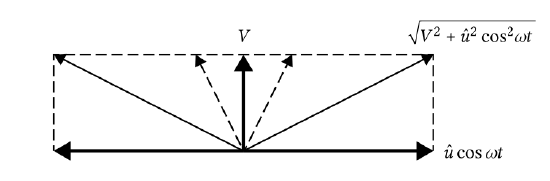
In the cross-shore direction, the time-averaged (not the instantaneous) bed shear stress is zero. With the above approximations, the time-averaged bed shear stress in the alongshore direction reads:
If we further assume that \(V \ll \hat\) this can be simplified to:
With \(\hat\) in shallow water given by Eq. 5.4.1.2 and with a constant ratio of wave height over water depth across the entire surf zone we find:
Analytical model for longshore current (no lateral dispersion)
For steady conditions the alongshore velocity follows from the balance between the driving force and the resisting friction force (Eq. \(\ref\)). This yields with Eq. \(\ref\)) and Eq. \(\ref\)):
The magnitude of the depth-averaged longshore current velocity varies in the surf zone as a function of the dissipation, wave height and water depth. The dissipation and wave heights can be modelled using a wave model (with roller model). In our simple dissipation model \(\gamma = H/h\) = constant and we can write the force balance Eq. \(\ref\) as:
For a constant beach slop \(\tan \alpha = -d h_0/dx\) and for \(dh/dx \approx dh_0/dx\), the current velocity is proportional to the depth with a maximum at the breaker line (where \(h = h_b\)):
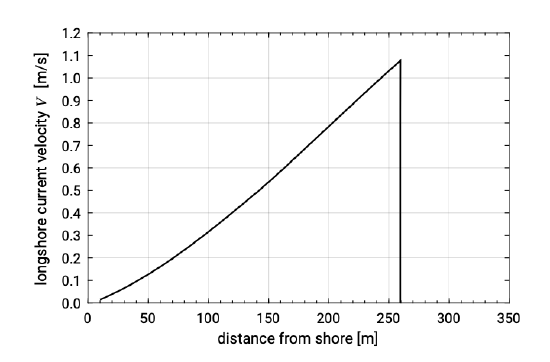
A longshore current profile according to Eq. \(\ref\) is shown in Fig. 5.39. The larger the wave height \(H_b\) at breaking, the larger the maximum longshore current velocity and the wider the littoral zone; a factor 2 larger wave height, would then result in a factor 8 larger discharge in the surf zone. Eq. \(\ref\) also allows us to get an idea of the effect of the beach slope \(\tan \alpha\). A steeper slope, on the one hand, results in (linearly) higher velocities. On the other hand the width of the surf zone becomes linearly smaller. The discharge through the entire surf zone is then constant to a first approximation (we have amongst others neglected the effect of the beach slope on the breaking parameter, Sect. 5.2.5). If the wave angle is small, the longshore current velocity at a specific water depth within the surf zone, becomes a linear function of \(\varphi_0\) (since: \(\sin \varphi_0 = \varphi_0\) for small \(\varphi_0\)).
Turbulent forces redistributing momentum
So far, the effect of lateral dispersion of momentum by turbulence has been ignored. Including turbulence in the momentum equation tends to smooth out velocity gradients (including the unrealistic velocity gradient at the breaker point).
Let us first look at turbulence and turbulence modelling in a bit more detail. In Sect. 5.4.3, the total velocity vector was said to be composed of a mean, a wave and a turbulent part. The turbulent shear stress was subsequently defined as the stress introduced when averaging over the turbulent motion. In analogy with the modelling of viscous stresses, in a turbulent flow the shear stress is generally related to velocity gradients through a turbulent or eddy viscosity \(v_T\). The molecular viscosity \(v\) seems to make water sticky and resist flowing and may be thought of as a measure of viscous fluid friction. Similarly \(v_T\) is a measure of turbulent fluid friction (in coastal waters \(v_T \gg v\)). The eddy viscosity \(v_T\) [\(m^2/s\)] depends on a characteristic spatial scale and on a characteristic velocity. In the littoral zone, both are related to the wave motion. The wave orbital motion, for instance, can be regarded as a measure for the characteristic velocity. For vertical mixing, the characteristic (mixing) length is the depth. Horizontal mixing is not restricted by water depth. For that reason, in nearshore modelling the horizontal eddy viscosity \(v_T, H\) is often taken much larger than \(v_T\) for vertical mixing. Typical values for the eddy viscosity \(v_T\) are \(10^ m^2/s\).
We have seen that the driving force for the longshore current is \(\partial S_ \partial x\). The shear component of the radiation stress \(S_\) was defined through Eq. 5.5.2.5, in which the velocity components are due to the orbital motion. In analogy with Eq. 5.5.2.5 we can write for the turbulent force:
where the overbar now represents averaging over the turbulent motion (indicated with primes). This shear stress or friction force per unit surface area, acts on a surface parallel to the coast. It can be modelled as:
The eddy viscosity \(v_T\) [\(m^2/s\)] is also referred to as horizontal diffusivity.
The momentum equation in the alongshore direction now reads:
\[\dfrac \sin \varphi_0 + \dfrac \left (h \rho v_ \dfrac \right ) = \bar_\]
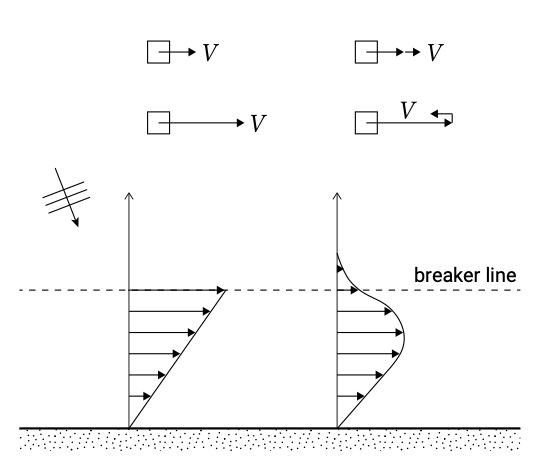
The effect of turbulent forces, smoothing the longshore current profile, is indicated in Fig. 5.40. Since the largest velocity gradient occurs at the breaker line, the maximum transfer of horizontal momentum will occur here. This leads to a reduction in the maximum velocity, a landward shift of the position of maximum velocity and to a situation where also outside the breaker zone longshore current velocities occur. The cross-shore distribution of the eddy viscosity now also determines the velocity distribution.
Roller momentum
Section 5.5.4 discussed that the measured onset of set-up occurs closer to the shore than predicted. This spatial lag was attributed to the roller momentum that had not been taken into account. Similarly longshore current velocity profiles show an onshore shift in the maximum longshore current velocity. This can be modelled by including the roller contribution in the alongshore momentum equation.
Irregular waves
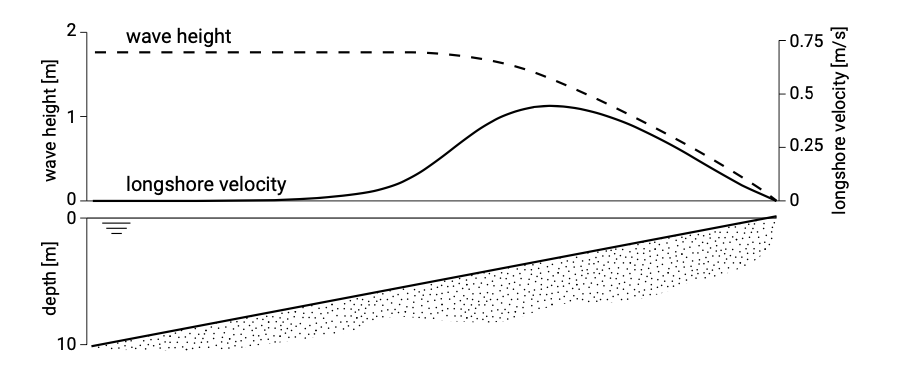
Until now we have only considered regular waves. In reality, of course, waves are irregular and there is no sharply defined breaker line. The effect of wave irregularity is therefore to smooth out the velocity distribution, very similar to the effect of turbulence, giving a wider and less sharply peaked velocity distribution. This is also illustrated in Fig. 5.41, which shows the output of a computation with the computer model Unibest-CL+.
Profile with breaker bar

If we have a coastal profile with a breaker bar, then the determination of the velocity distribution gets more complicated. In a simplified approach, we can distinguish between a breaker zone at the seaward side of the breaker bar (if waves indeed break at the corresponding water depths) and a breaker zone near the shoreline where the remaining wave energy is dissipated. This simplification would lead to a zero long- shore current velocity in the deeper section between both breaker zones. Also in such a situation, both lateral transfer of horizontal momentum and the irregularity of the waves will smooth out the velocity distribution. An example of the longshore current distribution is given in Fig. 5.42. Wave breaking tends to concentrate on the bars and at these locations a longshore current is driven. For the highest wave condition, wave breaking already occurs at the outermost bar, whereas for the lowest wave condition wave breaking occurs only at the innermost bar and close to the shoreline.
This page titled 5.5.5: Alongshore balance-longshore current is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Judith Bosboom & Marcel J.F. Stive (TU Delft Open) via source content that was edited to the style and standards of the LibreTexts platform.